Diferencia entre revisiones de «SEPTIEMBRE 2000 A»
m (1 revisión) |
|||
| Línea 66: | Línea 66: | ||
=== Otros artículos de su misma categoría === | === Otros artículos de su misma categoría === | ||
| − | [[Categoría: | + | [[Categoría:PAU_SEPTIEMBRE]] |
Revisión actual - 22:13 19 may 2014
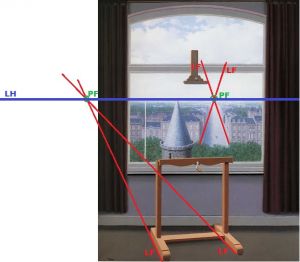
5.- Les Promenades d’Euclide, de René Magritte, 1953.
Indicar los elementos geométricos que se encuentran en la reproducción propuesta:
Sistema de representación, señalando la línea del horizonte y los puntos de fuga, si existen.
Presencia de módulos, polígonos, curvas, tangencias y simetrías. (2 PUNTOS)
Sistema de representación
Nos encontramos ante una perspectiva cónica como sistema de representación. Podemos determinar dos puntos de fuga que determinan la línea del horizonte. Si los pies del caballete se encontraran perpendiculares al plano de cuadro podríamos llamar a esta perspectiva "cónica frontal", pues las lineas de estos fugarían al mismo punto que la calle y esta es la denominación que se emplea para perspectivas con un solo punto de fuga. Al encontrarse oblicuos o girados respecto al plano de cuadro el punto de fuga de estos se desplaza hasta salirse del espacio gráfico de la obra obteniendo así un segundo punto de fuga.
Módulos
El módulo más importante es el de las ventanas de los edificios que se observa a través de la ventana, son módulos arquitectónicos que son rectángulos y al encontrarse en posición frontral se siguen observando como rectángulos. También se podría destacar los ladrillos de la torre de base circular que son rectangulares aunque van variando la forma que percibimos según que parte de la torre observemos.
Polígonos
Hay varios polígonos:
1.- Las ventana de los edificios que se observan frontalmente son rectángulos y se ven como tal. En cambio las ventanas que están en las paredes laterales siguen siendo rectangulares, pero son vistas como trapecios.
2.- La ventana desde la cual se ve el paisaje también es rectangular y se ve como tal.
3.- La mayor parte de los tejados tienes forma de trapecio y se observan también como trapecios cuando se ven con esta perspectiva cónica.
curvas
La base del cono que hay encima de la torre es una circunferencia, que al ser vista mediante la perspectiva se ve como una elipse (curva cónica).
tangencias
Aunque no se aprecia muy bien por que la tangencia está un poco tapada, debe haber una entre la base elíptica del cono y la torre. Son dos tipos de tangencias: 1-rectas tangentes a una elipse por un punto exterior, el cono del tejado de la torre. 2- Rectas con una dirección determinada (en este caso vertical) tangentes a una elipse, el cilindro de la torre.
También apreciamos ciertos enlaces de curvas en uno de los listones, en posición frontal del caballete.
simetrías
La habitación que está en el primer plano es simétrica, el eje de la cual (axial) pasa por el centro. La calle también es simétrica.
Otras consideraciones
Este cuadro tiene ocultas algunas consideraciones interesantes sobre perspectiva.
En primer lugar Magritte nos enseña una forma de comprobar que una perspectiva ha sido correctamente efectuada. Esta comprobación consiste en interponer la representación entre el punto de vista y la escena. Si, guiñando un ojo, los bordes de la representación encajan con el resto de la escena, la representación será correcta. Con este procedimiento lo que haríamos sería hacer coincidir el soporte de la obra con un plano de cuadro imaginario empleado para la representación.
Por otro lado Magritte está jugando con nuestra percepción de la profundidad, situando un cono quyo vértice se posa sobre la linea del horizonte. Las generatrices del contorno aparente del cono muestran el mismo ángulo que los márgenes de la calle que fuga hasta la linea del horizonte. Magritte de este modo sugiere una posible confusión entre lo que fuga y lo que es un volumen.
No es posible que las lineas de dos calles que siguen una misma dirección fuguen en dos puntos distintos.
Enlaces externos
Usuarios que han colaborado en este artículo
Bryan G. Ximo 1,8